Contenu
Informations méthodologiques
Informations méthodologiques et interprétation des analyses des valeurs extrêmes ainsi que du diagramme des intensités à l’exemple des stations de Genève-Cointrin et Lugano.
Informations méthodologiques et interprétation des analyses des valeurs extrêmes ainsi que du diagramme des intensités à l’exemple des stations de Genève-Cointrin et Lugano.
Selon la théorie des valeurs extrêmes, les valeurs les plus élevées d’une quantité (par exemple précipitations journalières ou rafales sur 1s) prises chacune sur des intervalles de même longueur peuvent être employées pour déduire le comportement extrême de cette quantité, c’est-à-dire à des niveaux dépassant tout ce que nous avons vécu. Ces maximums sont dits suivre la loi du maximum d’un échantillon, connue en anglais sous le nom de Generalized Extreme Value distribution et abréviée ci-dessous par (GEV). Les observations utilisées pour les analyses des valeurs extrêmes présentées sur ce portail web sont par conséquent des maximums saisonniers et/ou annuels.
L’inférence Bayésienne a été employée pour estimer les niveaux de retour. L’avantage de cette approche est qu’elle tient compte d’emblée des incertitudes.
Nous estimons un ensemble de distributions GEV toutes compatibles avec les observations. Dans la pratique, cet ensemble est constitué d’un grand nombre de distributions simulées, par exemple mille, chacune desquelles fournit une estimation d’un niveau de retour.
Pour une période de retour donnée, nous obtenons par conséquent non pas un niveau de retour, mais une distribution de niveaux de retour. Pour chaque période de retour sur le diagramme des niveaux de retour (i.e. pour chaque position sur l’abscisse), le niveau de retour représenté (le point correspondant sur la courbe bleue) est la médiane des niveaux de retours calculés pour cette période de retour particulière à partir de toutes les GEV estimées.
Une conséquence importante de cette procédure est que la courbe bleue représentée sur le diagramme des niveaux de retour n’est plus une distribution GEV. Néanmoins, comme de coutume, pour une période de retour donnée, par exemple 50 ans, la valeur de la courbe bleue en ce point, disons 80mm/jour, peut être interprétée comme la quantité de précipitations dépassée seulement environ 20 fois en 1000 ans (avec le même climat).
Un grand avantage de l’inférence Bayésienne est que les intervalles de confiance peuvent être interprétés de façon intuitive : il y a 95% de chances que la vraie valeur du niveau de retour se trouve entre les bornes d’un intervalle de confiance à 95%.
Lorsque nous appliquons la théorie des valeurs extrêmes aux maximums annuels, nous supposons tacitement que les processus menant aux précipitations en une année donnée restent les mêmes. Évidemment, ce n’est pas toujours le cas : les processus de précipitations dépendent souvent de la saison. Autrement dit, en utilisant les maximums annuels pour estimer les niveaux de retour, il est possible que nous ne respections pas les conditions nécessaires pour une estimation fiable.
Afin d’éviter cela, nous estimons d’abord les niveaux de retour saison par saison, à partir des maximums saisonniers, puis nous dérivons numériquement le niveau de retour annuel à partir des niveaux de retour saisonniers.
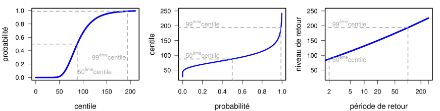
Le diagramme des niveaux de retour représente la probabilité qu’une valeur donnée soit dépassée. Cette probabilité est exprimée en années. Ainsi, on s’attend à ce qu’une valeur qui a une probabilité de 1% d’être dépassée en une année donnée sera dépassée en moyenne (sur une très longue période) une fois tous les 100 ans. Alors, on dit que la valeur en question, dite « niveau de retour» ou « valeur de retour » a une « période de retour » de 100 ans, autrement dit est centennale. En fait, les niveaux de retour sont des « quantiles extrêmes » : la valeur de retour centennale a une probabilité de 0.99 de ne pas être dépassée, et correspond par conséquent au 99e centile (cf. informations supplémentaires).
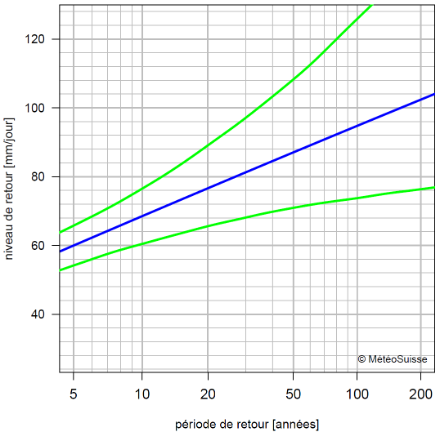
Afin de mettre en valeur le comportement des évènements les plus rares, les périodes de retour sont transformées de façon que les niveaux de retour correspondants se trouvent sur une ligne droite si les maxima annuels suivent une loi de distribution de Gumbel
(voir le repport).
Le diagramme des niveaux de retour permet de voir d’un coup d’œil le comportement des extrêmes. Il représente la probabilité de dépassement d’une grandeur, ici les cumuls de précipitations sur un jour à Lugano (ordonnée). Ces probabilités sont exprimées en nombre moyen d’années (abscisse).
Le comportement extrême des cumuls de précipitations sur un jour à la station de Genève-Cointrin peut être déduit du diagramme des niveaux de retour : l’estimation des niveau de retour (ligne bleue) a une courbure légèrement négative, ce qui suggère qu’au-delà d’un cumul journalier donné, la probabilité qu’un cumul soit dépassé est nulle. En revanche, la forte courbure positive de la borne de confiance supérieure nous révèle que ce comportement extrême est incertain : il est possible qu’un cumul de précipitations journalier quelconque ait une probabilité non nulle d’être dépassée, et cette probabilité décroîtrait assez lentement (i.e. de façon polynômiale). Par conséquent, même des évènements très rares auraient une probabilité non-négligeable d’être dépassés.
La série chronologiques des maximums annuels (1e figure de gauche) informe visuellement sur les données manquantes et sur de possibles tendances ou cycles dans les données. Ici, la variation dans les maximums annuels pourrait être aléatoire. L’histogramme (2e figure de gauche) montre la fréquence avec laquelle les maximums annuels ont été mesurés, et peut être entendu comme une densité de probabilité empirique.
Le diagramme Quantile-Quantile (1e figure de droite) nous renseigne sur la fiabilité de l’ajustement : si le modèle est adéquat pour les données, les quantiles empiriques doivent correspondre approximativement aux quantiles estimés, et ce surtout si l’échantillon est grand. Si c’est le cas, les points s’aligneront approximativement sur la diagonale. Si, par exemple, pour les quantiles élevés, les quantiles empiriques étaient systématiquement inférieurs aux quantiles estimés, cela suggèrerait que la queue de la vraie distribution décroisse plus rapidement que celle de la distribution estimée. A Genève-Cointrin, il n’y a pas de sous-estimation ou de surestimation systématique de la queue de la distribution. L’éparpillement des points de part et d’autre de la droite rouge pourrait éventuellement être réduit en modélisant explicitement le cycle annuel des cumuls journaliers des précipitations.
Sur le diagramme des niveaux de retour (2e figure de droite) on représente parfois par des points, nommés « plotting points » en anglais, les observations auxquelles on a conféré une période de retour empirique. La position de ces points sur l’ordonnée correspond à la valeur des maximums annuels. En revanche, comme la véritable période de retour de ces observations n’est pas connue, la position de ces points sur l’abscisse est calculée empiriquement en fonction de la taille de l’échantillon. Pour un échantillon de 50 années, on donnera au maximum annuel le plus élevé la période de retour d’environ 50 ans, au deuxième maximum le plus élevé une période de retour d’environ 25 ans, et ainsi de suite. Ainsi, la période de retour empirique ne représente en aucune façon le comportement local de la quantité d’intérêt (par exemple le cumul de précipitations journalier) à la station considérée, puisqu’elle serait la même quel que soit le lieu géographique. Néanmoins, certaines conclusions peuvent être tirées de la comparaison entre ces points et l’estimation des niveaux de retour (ligne bleue) : tout désaccord substantiel ou systématique entre les valeurs estimées au moyen de la GEV et ces valeurs empiriques suggère que le modèle n’est pas adéquat (mise à part l’erreur d’échantillonnage).
Chaque analyse des valeurs extrêmes est soumise à un test statistique pour déterminer sa fiabilité. Le verdict du test est alors cité sur la page principale. Ce verdict ne concerne pas l’incertitude de l’estimation due à la taille limitée de l’échantillon. Il décrit la possibilité que les hypothèses justifiant le choix du modèle statistique soient fausses.
Si les résultats sont non-fiables, par exemple, le modèle choisi représente très mal les valeurs extrêmes observées (les maximums annuels). Trois degrés de fiabilité ont été définis : non fiables, peu fiables, et fiables. La table ci-dessous montre comment les interpréter et que faire lorsqu’on y est confronté.
| Fiabilité | Interprétation | Que faire? |
| non fiables | Les valeurs extrêmes observées sont mal représentées par le modèle statistique. | Ne pas utiliser le modèle statistique. Utiliser les évènements observés les plus grands ou la station fiable la plus proche. |
| peu fiables | Les valeurs extrêmes observées ne sont pas bien représentées par le modèle statistique. Certaines hypothèses pourraient être fausses. | Une évaluation soigneuse s’impose. Utiliser les guides visuels (rapport technique, p.32) pour décider. Si les points ne s’éloignent pas systématiquement de la diagonale, procéder comme si les résultats étaient fiables, sinon comme s’ils étaient non fiables. |
| fiables | Les valeurs extrêmes observées sont bien représentées par le modèle statistique. | Le modèle statistique peut être utilisé. |
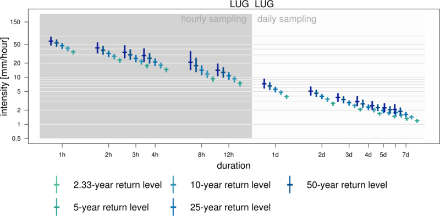
Le diagramme des intensités révèle le comportement des précipitations très intenses à différentes durées d’accumulation. Il est intentionnellement présenté de façon similaire aux diagrammes Intensité-Durée-Fréquence (IDF) d’usage en hydrologie, mais son contenu diffère de façon substantielle : les niveaux de retour représentés ici ont été estimés séparément pour chaque durée, à partir de données mesurées une fois par heure pour les durées infra-journalières, et une fois par jour pour les données supra-journalières. Aucune hypothèse n’a été faite concernant la relation entre les intensités de précipitations de différentes durées, et donc aucune dépendance entre elles n’a été utilisée pour déduire les niveaux de retour pour les courtes durées d’accumulation (voir Technical Report of MeteoSwiss 255 pour les détails).
Dans ce diagramme, l’abscisse et l’ordonnée ont toutes deux été soumises à une transformation logarithmique. De ce fait, les différences sont amplifiées pour les faibles intensités, et paraissent plus petites qu’elles ne le sont en réalité pour les fortes intensités. Cette transformation souligne le fait que l’intensité des précipitations diminue avec leur durée. Malheureusement, comme les intervalles de confiance subissent la même transformation, leur taille trompe l’œil, en particulier lorsqu’on essaye d’évaluer leur asymétrie de part et d’autre de la valeur de retour estimée.
La couleur de fond indique l’intervalle temporel de mesure des observations utilisées. En effet, les statistiques des durées infra-journalières sont faites à partir de maximums annuels de valeurs mesurées toutes les heures à la même heure (hh:40 - hh+1:40), et cumulées si nécessaire en sommes glissantes. De même, les estimations supra-journalières sont faites à partir de maximums annuels d’observations journalières, mesurées à heure fixe (5:40 - 5:40 UTC), et elles aussi cumulées si nécessaire en sommes glissantes.
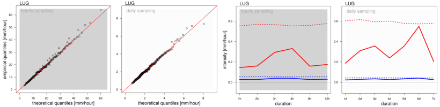
Sur les diagrammes du panneau de gauche, on peut s’attendre à ce que les points s’écartent de la diagonale çà et là, de façon aléatoire ; ils ne devraient néanmoins pas former un motif systématique, ni s’en éloigner trop. Comme les quantiles pour les courtes durées ont des valeurs plus élevées que pour les longues durées, ces diagrammes sont moins informatifs que pour les analyses de valeurs extrêmes de cumuls de précipitations sur une seule durée. En particulier, l’information concernant l’ajustement des intensités sur 3 à 12 heures, ainsi que sur 3 à 7 jours est limitée : dans l’exemple montré, il y a une légère indication que les niveaux de retour pour les intensités de 3 ou 4 heures soient peu fiables. En revanche, on ne constate pas, dans l’ensemble, de déviation systématique de la diagonale.
Sur le panneau de droite se trouvent des informations supplémentaires concernant la validité de l’ajustement et par conséquent une évaluation de la fiabilité des résultats. Si la ligne pleine se trouve au-dessus de la ligne pointillée, la validité de l’ajustement pour cette durée particulière est peu fiable. La statistique AD teste l’estimation des hauts niveaux de retour. Si l’erreur quadratique moyenne (RMSE) ne révèle que des déviations aléatoires (c.-à-d. que toutes les valeurs se trouvent en dessous de la ligne pointillée bleue), mais que la statistique AD se trouve au-dessus la ligne pointillée rouge, alors les niveaux de retour à faible période de retour pourraient être utilisés quand-même, tandis que ceux à hautes périodes de retour sont sans doute non fiables.
Ici l’erreur quadratique moyenne pour les intensités de précipitations sur 6 jours atteint la valeur critique. Par conséquent, pour cette durée de cumul, nous recommandons d’examiner soigneusement la comparaison des estimations des niveaux de retour avec les observations, et de consulter l’analyse des valeurs extrêmes des cumuls de précipitations sur 6 jours (si celle-ci existe et est fiable).
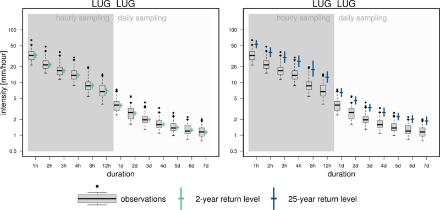
La comparaison des quantiles empiriques avec les estimations de niveaux de retour ayant une période de retour de 2 et 25 ans donne une idée de la qualité de l’ajustement en deçà de l’ intensité maximale déjà observée : à Lugano, le diagramme des intensités est basé sur 34 ans de données horaires et 50 ans de données journalières. Comme nous ne considérons que les maximums annuels, nous nous attendons à ce que le niveau de retour biennal soit proche de la médiane, c.-à-d. qu’environ la moitié des maximums annuels soit au-dessus, l’autre en-dessous du niveau de retour biennal. En revanche, nous nous attendons à ce que le niveau de retour ayant une période de retour de 25 ans ne soit dépassé qu’une ou deux fois pendant la période observée. Ainsi, en moyenne sur toutes les durées infra-journalières ce serait presque 1.4 fois par durée de cumul ; pour les données supra-journalières, ce serait presque 2 fois pour chaque durée. Pour les deux périodes de retour, la comparaison avec les observations ne révèle pas de problèmes avec la validité du l’ajustement.
Chaque analyse des valeurs extrêmes des intensités de précipitations est testée pour sa fiabilité, et le verdict est cité sur la page principale. Ce verdict ne concerne pas l’incertitude inhérente à l’estimation à partir d’un échantillon de taille limitée. Il décrit la possibilité que les hypothèses justifiant le choix du modèle statistique soient fausses.
Si par exemple les résultats sont peu fiables, le modèle ne représente pas bien les intensités de précipitations extrêmes observées pour certaines durées de cumul. Trois degrés de fiabilité ont été définis : non fiable, peu fiable, et fiable. La table ci-dessous montre comment les interpréter et que faire lorsqu’on y est confronté.
| fiabilité | interprétation | Que faire? |
| non fiables | Les intensités extrêmes observées sont mal représentées par le modèle pour quelques durées de cumul. | Ne pas utiliser les estimations des niveaux de retour. Utiliser les boîtes à moustaches des maximums annuels observés pour une première impression; consulter les analyses des valeurs extrêmes des cumuls de précipitations si celles-ci existent et sont fiables. Si certaines durées ne présentent pas de problèmes, les estimations peuvent être utilisées avec prudence. Sinon, utiliser la station fiable la plus proche. |
| peu fiables | Les intensités extrêmes observées ne sont pas bien représentées par le modèle pour quelques durées de cumul. | Une évaluation soigneuse est recommandée. Vérifier la qualité d’ajustement au moyen des guides visuels présentés. Si seules certaines intensités sont d’intérêt: vérifier si celles-ci présentent des problèmes particuliers. Si elles n’en présentent pas, utiliser les estimations, sinon utiliser la station fiable la plus proche. |
| fiables | Les intensités extrêmes observées sont bien représentées par le modèle pour la plupart des durées de cumul. | Les estimations des niveaux de retour peuvent être utilisées. Dans l’ensemble, le maximum annuel des intensités de précipitations est bien représenté par les distributions estimées pour la plupart des durées de cumul. |