Navigation rapide (Clés d'accès)

Contenu

La circulation générale de l’atmosphère (2ème partie)

MétéoSuisse-Blog | 22 septembre 2024
5 Commentaire(s)

Partant de l’idée que la rotation de la Terre est absolument centrale pour expliquer la façon dont l’atmosphère se comporte à la surface de notre planète, nous avons – dans l’article du 18 septembre 2024 de notre blog – abordé la circulation générale de l’atmosphère en considérant la façon dont le mouvement circulaire est traité en physique, en particulier au moyen des concepts de « quantité de mouvement » et de « moment angulaire ». La partie d’aujourd’hui s’intéressera aux mouvements rotatifs de l’atmosphère en mettant en avant les idées de tourbillon absolu et de tourbillon relatif. Nous verrons que ces notions sont intimement reliées à un autre phénomène, évoqué quant à lui dans l’article du 14 mars 2024 : la force de Coriolis.

  • Météo

Pied de page

Navigation top bar

Toutes les autorités fédéralesToutes les autorités fédérales

Navigation des services

La « vorticité » définit – selon le dictionnaire Larousse – la qualité de ce qui tourbillonne. C’est ce terme, plus habituel lorsque l’on parle du comportement de l’atmosphère, que nous utiliserons dans cet article en lieu et place du mot « tourbillon ».

Si, debout dans votre pièce, vous faites un tour sur vous-même, vous donnez à votre corps une certaine vorticité ; cette dernière est maximale car l’axe de rotation se confond avec l’axe vertical de votre corps. Il n’est cependant pas nécessaire que les deux axes soient superposés, il suffit qu’ils soient parallèles pour que la vorticité soit maximale. Sur un carrousel par exemple, que vous soyez au centre du carrousel ou sur son bord, la vorticité est la même puisque vous effectuez un tour complet sur vous-même durant le même laps de temps (l’axe de rotation du carrousel est parallèle à l’axe vertical de votre corps) ; ce qui change en revanche, c’est la vitesse de déplacement autour de l’axe, de plus en plus grande au fur et à mesure que vous vous éloignez du centre, comme nous l’avons vu dans la première partie de cette série d’articles. Par convention, en météorologie on qualifie la vorticité de positive lorsqu’elle se fait dans le sens inverse des aiguilles d’une montre (cyclonique dans l’hémisphère nord) et négative dans le sens horaire (anticyclonique dans l’hémisphère nord). Sa valeur augmente proportionnellement à la vitesse de rotation.

Mais la Terre n’est pas un carrousel (donc un disque), c’est une sphère et cela change tout. Si vous êtes au Pôle, l’axe de rotation de la Terre est parallèle à l’axe vertical de votre corps, mais si vous entamez un voyage en direction de l’équateur, l’axe de votre corps va insensiblement s’écarter de l’axe de rotation de la Terre, jusqu’à en être non plus parallèle mais perpendiculaire. A ce moment-là, votre vorticité sera égale à zéro. En effet, une personne debout à l’équateur n’effectue qu’une translation autour du globe, mais pas l’ombre d’un tour sur elle-même. En résumé, plus vous vous éloignez du pôle, plus vous tournez rapidement autour de l’axe de rotation, mais moins vous tournez sur vous-même. Et pour les masses d’air ? C’est exactement la même chose…

Le lien entre la vorticité et la latitude est donné en physique par la formule mathématique suivante :

Vorticité = 2ΩsinΦ (où Ω représente la vitesse angulaire de la Terre et Φ la latitude).

2Ω étant constant, on voit que la vorticité ne dépend que de la latitude. Cette formule est précisément nommée le « paramètre de Coriolis ».

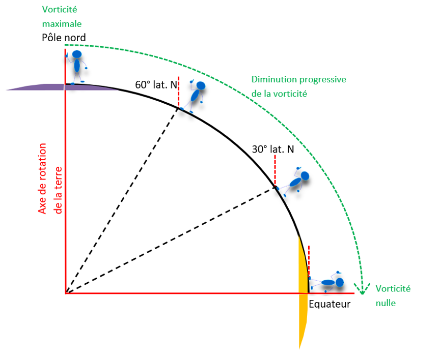
Deux éléments, très importants météorologiquement parlant, peuvent être déduits du schéma ci-dessus :

1. Au voisinage du pôle (disons sur un angle de 20° de part et d’autre), la vorticité est maximale et varie peu car la Terre peut quasiment être assimilée à un disque sur cette distance (aire mauve). La quantité de mouvement des masses d’air est en revanche très faible car elles sont proches de l’axe de rotation.

2. Au voisinage de l’équateur, la vorticité est nulle ou proche de zéro, en revanche la quantité de mouvement des masses d’air est importante en raison de la grande distance les séparant de l’axe de rotation de la Terre (aire orange).

Ces considérations seront primordiales lorsque l’on s’intéressera aux mouvements latitudinaux des masses d'air, soit de l’équateur vers les pôles et inversement.

Vorticité planétaire, vorticité relative et vorticité absolue

Lorsque deux ou plusieurs éléments se déplacent les uns par rapport aux autres, la description du mouvement nécessite au préalable de définir le cadre de référence de l’observateur. Si l’observateur est totalement extérieur aux éléments en mouvement, son point de vue est dit « absolu » ; s’il est lié à un de ces éléments, son point de vue est dit « relatif ». Ainsi par exemple, si vous roulez sur l’autoroute à 100 km/h d’ouest en Est et qu’un vent de 40 km/h souffle dans la même direction (vent d’ouest donc), relativement à vous il s’agira cependant d’un vent d'Est (de face) de 60 km/h.

Admettons que vous soyez en vacances au parc national du Mont Kenya, situé exactement sur l’équateur, par une belle journée sans vent. De votre point de vue, la vitesse de la parcelle d’air qui vous entoure est nulle, et pourtant cette parcelle d’air – liée à la Terre par la gravité – se déplace dans l’espace à la vitesse de 1674 km/h.

De la même manière, une masse d’air totalement immobile au pôle ne vous semblerait affectée d’aucune vorticité (si vous pouviez la ressentir…), alors qu’elle aura effectué en 24 heures un tour complet sur elle-même. Cette vorticité intégralement liée à la rotation de la Terre est dite « planétaire ».

Outre la vorticité planétaire, l’atmosphère en mouvement peut également être soumise à une vorticité liée à son déplacement propre. Cette vorticité est dite « relative », car le point de vue adopté est celui d’un observateur sur Terre ; elle est de deux ordres :

1. En lien avec la courbure des flux atmosphériques : cycloniques (vorticité positive) et anticycloniques (vorticité négative) :

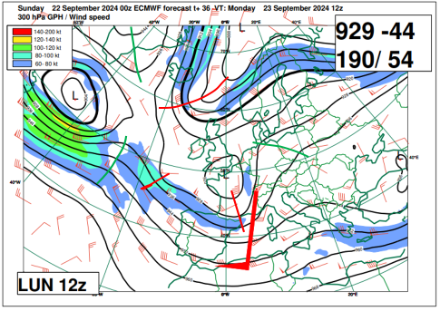
2. En lien avec la vitesse des flux atmosphériques. En effet, une différence de vitesse à l’intérieur d’un flux – même rectiligne – engendre des mouvements tourbillonnaires, comme le montre l’illustration ci-dessous. Pour vous en convaincre, placez un petit bout de bois dans un ruisseau, et vous verrez qu’il se mettra rapidement à tourner sur lui-même :

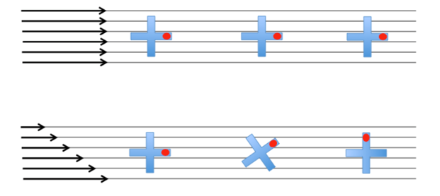
La somme des vorticités planétaire (Vp) et relative (Vr) donne la vorticité absolue (Va), ce que l’on peut écrire comme suit :

Va = Vp + Vr

La vorticité absolue constitue l’ensemble des mouvements tourbillonnaires tels qu’ils seraient perçus par un observateur situé dans l’espace. Tout comme le moment angulaire, la vorticité absolue d’une masse d’air est immuable en l’absence d’influence extérieure ; on dit qu’elle se conserve.

Dans notre 3ème partie, nous verrons que la circulation générale de l’atmosphère est déterminée en grande partie par la nécessité pour les masses d’air en mouvement de conserver cette vorticité absolue au fur et à mesure de leurs déplacements, en direction des pôles pour l’air d’origine tropicale ou en direction de l’équateur pour l’air polaire.

Ce sera le 11 octobre, et nous comptons sur vous 😉

Vous trouverez ici une intéressante expérience (facilement réalisable par vous-même) illustrant la vorticité dans un fluide (malheureusement en anglais, mais assez intuitive).

Liens :

- Circulation générale de l'atmosphère (1ère partie)

- La force de Coriolis

Portrait

MétéoSuisse est l’Office fédéral de météorologie et de climatologie. Nous prenons le pouls du temps et du climat pour que vous ne soyez pas dans le brouillard.

Informations sur cet accès internet