Navigation des services
Recherche
Imaginons un défilé militaire durant lequel les soldats passent devant nous par rangées de 20, parfaitement alignées. Au commandement « quart de tour à gauche », l’escouade effectue un changement de direction de 90° vers la gauche, les rangées restant toujours parfaitement alignées (pas si simple, ceux qui ont fait l’école de recrue le savent). Que va-t-il se passer concrètement ? Le soldat à l’extrême gauche de la rangée va effectuer un quart de tour vers la gauche en restant sur place alors que le soldat à l’extrême droite de la rangée devra nettement accélérer le pas pour rester aligné avec les autres soldats. Ainsi, pour une rotation d’un même angle de 90°, la distance à parcourir sera de plus en plus grande au fur et à mesure que l’on s’éloignera de l’axe de rotation matérialisé par le 1er soldat à l’extrême gauche ; or comme cette distance doit être parcourue durant le même laps de temps par tous les soldats (pour que la ligne ne se déforme pas), la vitesse (on parle de vitesse linéaire) croît en proportion lorsqu’on s’éloigne de l’axe.
Cet exemple montre qu’une vitesse de rotation ne peut pas être formulée en termes simples et habituels, comme des km/h par exemple, mais qu’elle doit être formulée en incluant l’angle parcouru. On parle donc dans ces cas-là de vitesse angulaire, soit l’angle parcouru par unité de temps ; et on la note en physique au moyen du symbole Omega (Ω). Pour l’exprimer, de nombreuses formulations sont possibles, des plus barbares (radians/seconde par exemple) aux plus simplement compréhensibles comme les tours/minutes de votre vélo d’appartement ou du moteur de votre voiture.
Vous êtes toujours là ? On continue…
Prenons l’exemple de la Terre, dont le mouvement est en réalité assez complexe dans les détails, mais qu’on peut simplifier comme suit : elle tourne deux fois plus lentement que la petite aiguille de votre montre, puisqu’elle fait un tour sur elle-même en 24 heures (donc Ω = 360°/24h). Aux pôles, la vitesse linéaire réelle d’une personne sera nulle puisqu’elle fera un tour sur elle-même ; à l’équateur en revanche, et sachant que le rayon de la terre est de 6378 km, la vitesse sera de 1674 km/h et la distance parcourue en 24 heures d’environ 40'000 km. Ce n’est pas rien…
Quantité de mouvement et moment angulaire
La suite se corse un peu, mais on peut y arriver, si on ne se laisse pas intimider.
Si une mouche se déplace à 30 km/h, ou s’il s’agit d’un wagon CFF bien rempli, on devine intuitivement que ce n’est pas la même chose (on peut aussi se placer sur la trajectoire pour mieux s’en convaincre). La différence entre les deux réside dans ce que l’on appelle la quantité de mouvement, soit le produit d’une masse (notée m) par sa vitesse (notée v). La quantité de mouvement d’un wagon se déplaçant à 30 km/h est donc infiniment plus grande que celle d’une mouche volant à la même vitesse.
Comme on l’a vu dans le chapitre ci-dessus – et pour une vitesse angulaire donnée – la vitesse linéaire réelle d’un objet en rotation dépend de sa distance à l’axe de rotation. La quantité de mouvement de l’objet (qui inclut la vitesse) varie donc elle aussi en fonction de la distance à cet axe (le rayon noté r) : on appelle « moment angulaire » (ou moment cinétique) – noté L – la valeur incluant ce paramètre r à la quantité de mouvement, soit le produit de la quantité de mouvement par la distance à l’axe de rotation (L = mvr).
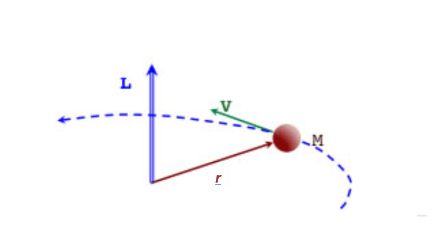
Si aucune force extérieure n’intervient, le moment angulaire d’un corps ne change pas. L’égalité L = mvr signifie donc que si l’un des trois paramètres mvr diminue, un autre de ces mêmes paramètres DOIT augmenter dans les mêmes proportions pour que le moment angulaire L reste inchangé.
L’illustration la plus classique de la conservation du moment angulaire est la vitesse de rotation d’une patineuse artistique (en l’occurrence Denise Bielmann) ; cette vitesse augmente au fur et à mesure que la patineuse ramène ses bras près de son corps. En langage mathématique, on dira qu’elle diminue r (son rayon) et que par conséquent v (sa vitesse de rotation) augmente pour que L (le moment angulaire) soit conservé.
Faites-en vous-même l’expérience au moyen d'un simple tabouret pivotant (mais bien huilé !) : asseyez-vous sur le tabouret et tournez le plus vite possible avec les bras et les jambes écartés, puis ramenez-les progressivement vers vous. La masse m restant constante (du moins durant ce laps de temps…) la vitesse de rotation v augmentera immédiatement, comme par magie.
Une autre expérience simple consiste à faire tourner autour de son doigt un objet attaché à une ficelle. Au fur et à mesure que la ficelle s’enroule autour du doigt (le rayon r diminue), la vitesse de l’objet augmente.
Et la météo dans tout ça ?
La vitesse angulaire de la Terre étant constante, le mouvement des masses d’air à la surface du globe est influencé par le fait qu’elles se rapprochent ou s’éloignent des pôles (donc qu’elles diminuent ou augmentent la distance à l’axe de rotation r). N’oublions pas toutefois que la Terre est une sphère et non un disque, ce qui complique un peu la donne.
Nous en reparlerons, si vous êtes toujours là, le dimanche 22 septembre.
D’ici là, bonne fin de semaine !