"Le battement d'ailes d'un papillon en Suisse peut-il déclencher une tornade en Oklahoma ?" Après une brève introduction à la théorie du chaos, nous tissons le lien avec les prévisions météorologiques et montrons pourquoi celles-ci sont difficiles à prévoir, même à court terme, en fonction de la situation météorologique.
En 1963, le météorologue Edward N. Lorenz découvre, par hasard, le comportement chaotique d'un système lors de ses expériences sur les courants convectifs.
Au cours de ses expériences, il chauffe des liquides et des gaz à l'aide une plaque chauffante. Il en résulte un courant dans lequel le liquide chauffé monte et se refroidit à nouveau à la surface, ce qui le fait redescendre. La montée et la descente du liquide se font en continu lorsque la plaque chauffante est allumée, ce qui entraîne la formation de courants convectifs ou de cellules de convection.
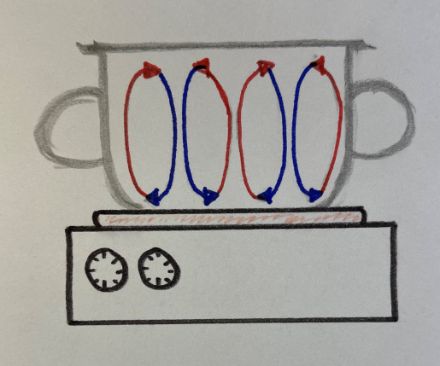
Lorenz a ensuite voulu décrire les flux à l'aide d'un modèle de prévision. Pour ce faire, il a lié la température et le taux de convection dans un système d'équations et a utilisé un ordinateur pour le résoudre. Lors de ses calculs ultérieurs, il a indiqué les conditions initiales du système d'équations avec seulement trois chiffres après la virgule, au lieu de six. Les résultats qu'il a obtenus étaient alors très différents de ses calculs précédents. Il avait découvert, par hasard, le comportement chaotique des systèmes.
Le système d'équations de Lorenz se compose de trois équations différentielles. Si l'on représente graphiquement les solutions du système d'équations de Lorenz, on obtient ce que l'on appelle un attracteur de Lorenz (voir l'image ci-dessous). Les axes X, Y et Z représentent les variables de l'équation. La ligne montre l'évolution des variables dans le temps, ce que l'on appelle une trajectoire. La solution graphique indique que la théorie du chaos n'est pas un chaos pur, mais un "chaos ordonné". La trajectoire tourne autour de deux points différents et il en résulte une structure assez semblable à celle d'un papillon. Cette structure est connue sous le nom d'attracteur de Lorenz.
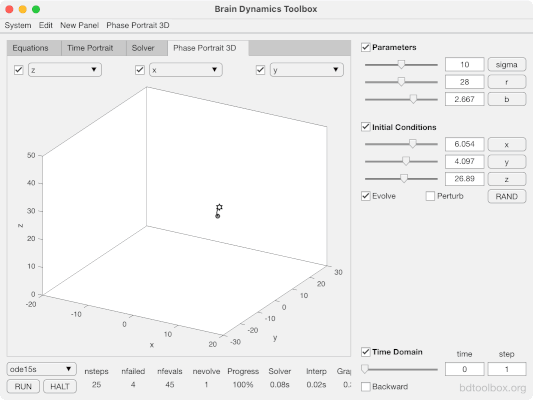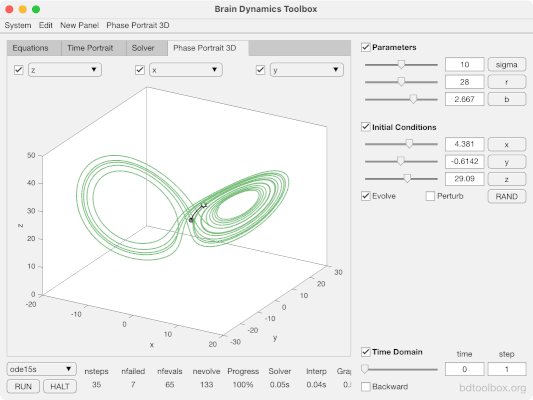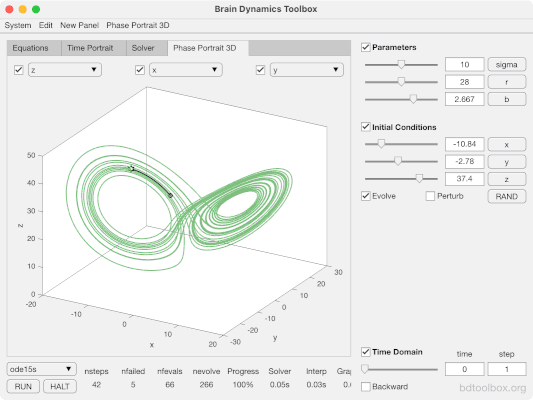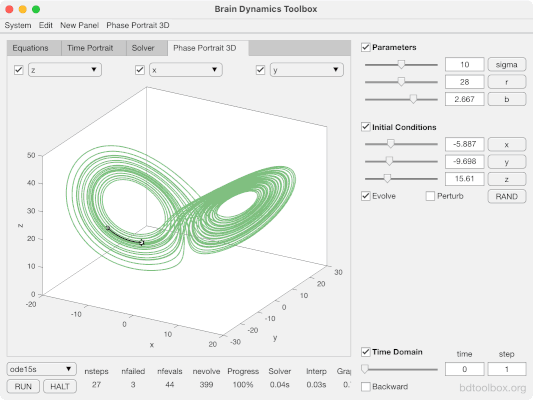
Le moment où le système bascule d'une orbite à l'autre est chaotique et dépend fortement des conditions initiales. Ce basculement est connu dans la théorie du chaos sous le nom de bifurcation.
De tels moments de basculement ou sauts existent également dans les prévisions météorologiques. Cela rend souvent difficile l'établissement de prévisions claires. En effet, les modèles météorologiques passent alors d'une solution à l'autre. Prenons un exemple :
La quantité de précipitations sur trois heures le mardi soir entre 18 et 21 UTC (20-23 h LT) est présentée ci-dessus. Les différents carreaux représentent les différents membres du modèle ICON-CH2. Les prévisions d'ensemble reposent sur des conditions initiales légèrement différentes et présentent des solutions en partie différentes. La question qui se pose maintenant est la suivante : y aura-t-il de la pluie mardi soir ? Certains membres montrent des signaux clairs de précipitations orageuses, d'autres au contraire indiquent un mardi soir sec. Cela illustre le fait que de petites variations des conditions initiales conduisent à des solutions différentes - dans ce cas, des orages ou des conditions sèches.
La saisie des conditions initiales est déjà entachée d'une certaine imprécision. Les mesures présentent toujours de petites imprécisions et nous n'avons pas assez de points de mesure pour saisir les conditions initiales de toute l'atmosphère. En outre, les équations des modèles météorologiques sont simplifiées, car il n'est tout simplement pas possible de décrire physiquement et mathématiquement l'ensemble des processus dans l'atmosphère. En outre, aucun ordinateur au monde ne serait capable de calculer tout cela dans les délais impartis.
Cela ne signifie pas pour autant que les prévisions météorologiques sont complètement chaotiques et imprévisibles. Mais cela montre que les moindres modifications des conditions initiales ont un impact important sur les événements météorologiques.
Chez MétéoSuisse, comme dans d'autres services météorologiques, nous essayons de mettre un peu d'ordre dans le chaos avec des prévisions d'ensemble.
Ci-dessous, vous pouvez voir les prévisions d'ensemble du modèle ECMWF pour le point de grille de Genève. Plus les lignes de température et de géopotentiel sont proches, plus la prévision est sûre. Cela signifie que malgré les différentes conditions initiales, la solution est la même. Il est dans la nature du système que plus le temps passe, plus l'incertitude augmente.
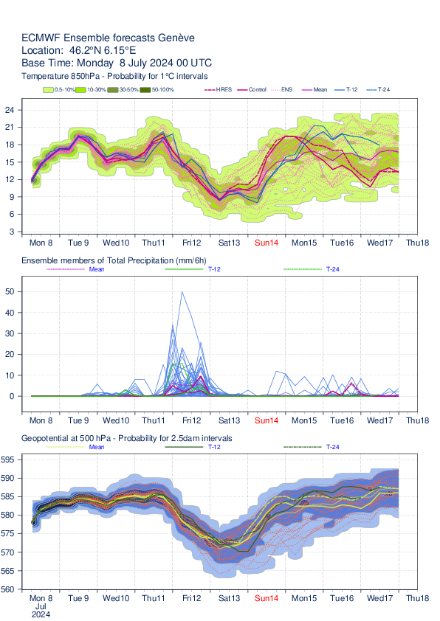
Même si les lignes de température et de géopotentiel sont relativement proches les unes des autres jusqu'au week-end, un examen plus attentif révèle de petites divergences. Ces différences apparaissent alors également dans les prévisions d'ensemble et sont généralement reproduites dans le bulletin météo avec des termes d'incertitude (pas exclu, possible, probable).
Ces derniers temps, nous avons eu beaucoup de situations météorologiques déterminées par de basses pressions, avec des averses et des orages. Ces processus sont extrêmement complexes et très chaotiques. Nous pouvons indiquer une situation d'averses et d'orages quelques jours à l'avance, mais pas le lieu et le moment exacts de ces évènements.
Mais avant que l'on ne s'y oppose : Si le temps ne peut pas être prévu, comment peut-on prévoir l'évolution du climat ?
Les modèles climatiques ou les prévisions à long terme diffèrent des modèles météorologiques. Ici, ce ne sont pas de prévisions détaillées pour certains jours ou certaines heures qui sont émises, mais ce qu'on appelle des tendances (probabilité qu'un mois donné soit trop chaud ou trop froid). Le modèle climatique est également soumis à d'autres processus, comme par exemple les interactions terre-atmosphère-océan couplées ou la prise en compte de l'ensemble de la couche atmosphérique.
La fameuse métaphore (qui a été quelque peu adaptée plus haut) d'après laquelle un battement d'ailes au Brésil peut déclencher une tornade au Texas, est connue sous le nom de l'effet papillon. Avec cette métaphore, Lorenz voulait attirer l'attention sur la complexité des systèmes et sur le fait que les moindres changements peuvent conduire à des résultats très différents.
Ce blog a été inspiré par le thème de la journée du DWD, service météorologique allemand, le 09 septembre 2020.
https://www.dwd.de/DE/wetter/thema_des_tages/2020/6/9.html