Navigation rapide (Clés d'accès)

Contenu

Les mathématiques : le langage de Dieu ?

MétéoSuisse-Blog | 22 août 2023
34 Commentaire(s)

En cette période de rentrée scolaire – et pour parler un peu d’autre chose que de canicule – nous vous invitons dans l’univers fascinant et injustement boudé des mathématiques. Surtout pas de panique ! Malgré le titre, soulignons que la totalité de cet article est accessible même aux grands traumatisés des maths. La partie qui fâche a été reléguée en toute fin d’article et peut sans conséquence être éludée. Allons-y !

  • Météo

Pied de page

Navigation top bar

Toutes les autorités fédéralesToutes les autorités fédérales

Navigation des services

Ceux qui ont des enfants savent que la plupart sont difficiles à motiver lorsqu’il s’agit des maths. C’est compliqué et ça ne sert à rien ! Pourtant, derrière cette matière cryptique et difficile d’accès se cache une des plus grandes conquêtes de l’humanité, et probablement l’une des principales clefs pour comprendre l’univers dans lequel nous vivons.

Galilée fut le premier à déclarer que « l’univers est écrit en langage mathématique ». De fait, il existe une adéquation étonnante entre les mathématiques et les phénomènes naturels, à tel point que bon nombre de physiciens estiment que les mathématiques n’ont pas été inventées mais découvertes par l’homme … nuance de taille ! Les équations mathématiques ne décriraient pas les phénomènes naturels, mais en seraient le fondement-même. Cet article va tenter d’illustrer cela par un exemple se rapportant à la météo.

Le pouvoir des mathématiques vis-à-vis de la nature n’est pas seulement explicatif, mais également prédictif.  Les équations de la physique ont ainsi à maintes reprises – dans l’histoire des sciences – permis de faire des découvertes théoriques précédant, parfois de très loin, la découverte « physique » et expérimentale de tel ou tel phénomène. Ce fut le cas par exemple de la planète Neptune, découverte en 1846 sur la base de calculs mathématiques préalables, ou encore de la déviation de la lumière dans un champ de gravité, prévue par Einstein en 1915 et observée par Arthur Eddington lors d’une éclipse solaire le 29 mai 1919, ou enfin plus près de nous de la découverte du boson de Higgs en 2012 (image ci-dessus).

Comme toutes les sciences, la météorologie fait appel à des équations mathématiques assez élaborées. Il arrive pourtant que certains phénomènes trouvent une explication dans une formulation mathématique relativement simple. C’est le cas par exemple de la circulation des vents autour d’une dépression ou d’un anticyclone. En effet, l’équation qui définit cette circulation est une équation classique du second degré, de laquelle nous pouvons tirer des conclusions étonnantes.

L’équation du vent de gradient

Le vent de gradient est un vent résultant de l’équilibre entre trois forces : la force du gradient de pression, la force de Coriolis et la force centrifuge liée à la courbure du flux autour d’une dépression ou d’un anticyclone. En atmosphère libre, où la force de friction est quasi-nulle, ce vent de gradient est pratiquement équivalent au vent réel observé.

L’équation qui décrit ce vent peut être ramenée au type : ax2 + bx + c = 0, enseignée assez précocement en classes de maturité, et dont la solution est double :

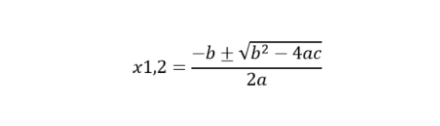
* pour plus de détails sur cette équation, se reporter à la fin de l’article

Il ressort de cette équation une chose intéressante :

Le rayon de courbure d’un anticyclone possède une limite théorique minimale en rapport avec la vitesse du flux qui le contourne. Autrement dit, plus le flux est rapide, plus le rayon de l’anticyclone doit être grand. Dit en d’autres termes encore, pour un rayon de courbure donné, la vitesse du flux ne peut pas être supérieure à une valeur limite maximale. Ceci explique pourquoi les isobares ne peuvent pas être serrés autour d’un anticyclone, en particulier près du centre où le rayon de courbure est le plus petit.

A l’inverse, il ressort de cette équation qu’autour d’une dépression il n’y a aucune restriction théorique à la force du gradient de pression, raison pour laquelle de profondes dépressions, des cyclones ou encore des tornades sont possibles.

Illustration de ce principe par les extrêmes

Les zones de basse pression

Dans le cœur d’un ouragan par exemple, les isobares sont tellement serrés qu’il devient presque impossible de les dessiner sur une carte, comme le montre l’exemple ci-dessous :

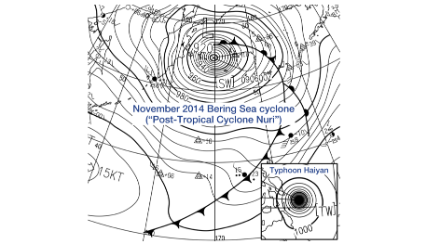
Ces deux exemples extrêmes suffisent à montrer que les dépressions ne sont effectivement soumises à aucune limite dans leur creusement, et que l’on pourrait imaginer des dépressions encore plus profondes que celles illustrées ici.

Les zones de haute pression

Le record homologué à ce jour pour une haute pression est 1083.8 hPa le 31 décembre 1968 au-dessus de la Sibérie (région d’Agata, 261 m).

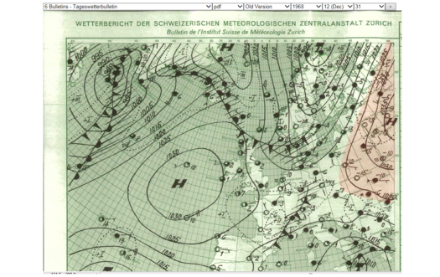
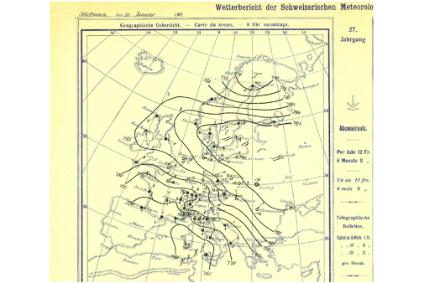
Conclusion

Il n’est pas difficile de s’apercevoir « empiriquement » qu’un anticyclone, quelle que soit sa force, se présente toujours sur les cartes météo sous la forme d’une vaste colline plus ou moins pentue à sa marge, alors que les dépressions peuvent être représentées sous la forme de véritable gouffres aux pentes quasi-verticales. Pour en comprendre la raison cependant, il est nécessaire de faire appel aux mathématiques ; un mathématicien n’ayant jamais vu une carte météo pourrait du reste découvrir ces caractéristiques avec certitude. Cet exemple n’est de loin pas isolé, c’est pourquoi dans les sciences de la nature, lorsque l’on veut répondre non plus seulement à la question « quoi ? » mais aux questions « pourquoi ? » et « comment ? », les mathématiques deviennent incontournables.

L’adéquation des mathématiques au réel et à la nature rejoint le vaste problème philosophique concernant le monde des idées et le monde empirique, vieux de plus de 2000 ans. Les mathématiques sont-elles le « langage de Dieu » comme le suggérait Newton ? Cette adéquation est-elle le fruit du hasard ou de la nécessité ?

Nous nous garderons bien de trancher ! Le problème de l’immanence ou de la transcendance des lois de la physique se trouve aux frontières de la science.

Comprenne qui peut, croie qui veut…

* Equations du vent de gradient :

Dans l’équation du vent de gradient anticyclonique ci-dessous, on voit que si R tend vers 0 (rayon de courbure de plus en plus petit), alors la fraction G/R tend vers l’infini, or comme cette valeur est soustraite à un nombre constant positif sous la racine carrée, on aboutirait à terme à la racine carrée d’un nombre négatif, ce qui est impossible. On voit donc que G et R sont liés et que la fraction ne peut pas dépasser une certaine limite (égale au premier membre de la racine carrée) ; cela signifie que si le rayon de courbure R diminue, le gradient de pression G doit diminuer dans de mêmes proportions pour que la valeur de la fraction soit conservée. De même, si le gradient de pression G augmente, R doit augmenter également pour que la valeur limite ne soit pas dépassée.

Dans l’équation du vent de gradient cyclonique en revanche, cette limite n’existe pas car la fraction G/ R est toujours additionnée au membre constant sous la racine carrée, laquelle reste donc toujours positive. R peut donc théoriquement tendre vers zéro… et le vent V vers l’infini !

R = rayon de courbure de la trajectoire (variable)

G = gradient de pression (variable)

ω = vitesse angulaire de la Terre (constante)

ϕ = latitude (quasi-constante)

ρ = densité de l’air (quasi-constante à une altitude donnée)

Pour approfondir :

Portrait

MétéoSuisse est l’Office fédéral de météorologie et de climatologie. Nous prenons le pouls du temps et du climat pour que vous ne soyez pas dans le brouillard.

Informations sur cet accès internet