Certains mots ont le don de faire le vide autour d’eux, de faire détaler comme des lapins tous ceux qui les considèrent d’emblée et a priori comme incompréhensibles. Dans les sciences mathématiques, ces mots sont légions ; par exemple « physique », « équations », ou même « mathématiques » d’ailleurs. La terminologie statistique n’échappe pas à cette règle, et des mots comme « quantile », « médiane », « écart-type », etc… sont des repoussoirs avérés.  D’ailleurs vous n’êtes peut-être déjà plus là !

Pourtant, quel élève de 10 ans n’a-t-il pas calculé lui-même sa « moyenne » pour se préparer psychologiquement à une éventuelle remontée de bretelles en remettant son bulletin à ses parents ? Eh bien, les autres termes recouvrent des concepts tout aussi simples. Ne nous laissons donc pas effrayer par le mot, passons outre et abordons l’idée.

Cela n’aura échappé à personne, l’expression des prévisions météo tend à abandonner le mode déterministe (il fera tel ou tel temps) au profit du mode probabiliste (la probabilité d’avoir tel ou tel temps est de tant). Cela se traduit dans les bulletins par des termes tels que « possible », « probable », « pas exclu » et dans les graphiques ou les cartes de prévision par des fourchettes de valeurs (comme dans la courbe des températures de notre application) ou par l’emploi de pourcentages (probabilité de dépasser certains seuils par exemple).

Quoi qu’on puisse en penser, cette évolution n’a pas pour but de noyer le poisson ou d’affranchir les météorologues de toute responsabilité vis-à-vis des utilisateurs, mais elle correspond simplement à une réalité : les conditions atmosphériques initiales ne pouvant pas être connues avec exactitude, les conditions futures (la prévision) ne le peuvent pas non plus. Il existe toujours plusieurs variantes, plus ou moins probables. Les prévisions d’ensemble permettent de visualiser ces variantes sous la forme de membres, et de les classer pour évaluer leur probabilité. Ce classement utilise des termes comme « moyenne », « médiane », « écart-type » ou encore « quantiles » qu’il est nécessaire de maîtriser pour comprendre la prévision. Ce sont ces termes que nous nous proposons d’expliquer.

Définition des termes

Plusieurs fois par jour, le modèle IFS fait 51 prévisions à 10 jours en partant de la même heure, mais en changeant légèrement les conditions initiales ; ces 51 prévisions s’appellent des membres.

Prenons au hasard la commune de Crissier et les prévisions de précipitations en 24h pour un jour donné. Admettons maintenant que la répartition des précipitations pour Crissier selon les différents membres soit celle ci-dessous (elle est un peu idéalisée pour faciliter la compréhension) :

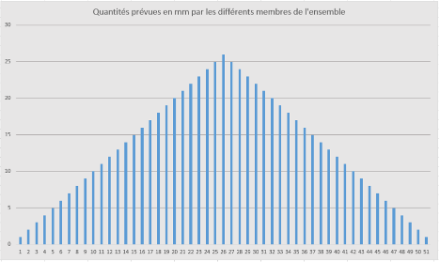
On voit que la répartition est régulière et symétrique autour de la valeur maximale de 26 mm représentée par le membre 26. Afin de mieux visualiser les différents termes statistiques, il est souvent très utile de commencer par classer les valeurs des différents membres dans l’ordre croissant (on appelle ça une « fonction de distribution cumulative »), ce qui donne la représentation ci-dessous, strictement équivalente à la précédente (on voit que chaque valeur est également représentée deux fois et que le maximum est 26 mm) :

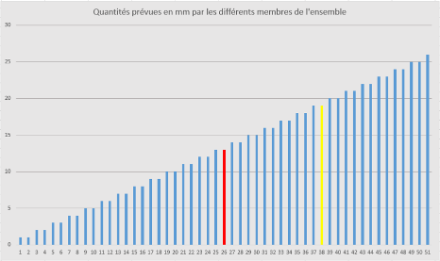
Voyons maintenant à quoi correspondent les termes statistiques mentionnés en introduction de cet article :

• La moyenne est le terme le plus simple, que nous maîtrisons tous depuis l’école primaire. Elle est obtenue en additionnant la valeur de tous les membres, puis en la divisant par le nombre de membres. Il s’agit donc d’une valeur unique dont la représentativité par rapport à l’ensemble peut fortement varier (cf. Ecart-type).  Dans la distribution ci-dessus, la moyenne est de 13 mm et est représentée par le membre 26 (en rouge).
• L’écart-type (en anglais « Standard Deviation ») mesure la dispersion des valeurs autour de la moyenne. En gros, il nous dit si la moyenne est représentative de l’échantillon. Plus l’écart-type est petit, plus la moyenne est significative. Dans la répartition ci-dessus, l’écart-type est de 7.4 mm, ce qui signifie que la moyenne de 13 mm n’est pas très représentative de l’ensemble. On peut dire d’une manière générale que plus l’écart-type est grand, moins la prévision est sûre.
• La médiane est la valeur qui coupe exactement en deux l’échantillon entre une moitié des membres donnant davantage de précipitations et l’autre moitié donnant moins de précipitations. Dans cet exemple, la répartition étant symétrique, la médiane est équivalente à la moyenne et est également représentée dans le graphique ci-dessus par le membre 26 donnant 13 mm (en rouge). Lorsque la répartition n’est pas symétrique, moyenne et médiane ne se confondent généralement pas.
• Les quantiles sont des pourcentages (généralement standards) regroupant un certain nombre de membres. Par exemple, le quantile 75 % (représenté par le membre 38 (en jaune) et valant ici 19 mm) nous dit que 75 % des membres prévoient moins de 19 mm et 25 % des membres prévoient davantage. Les quantiles les plus couramment utilisés sont les tranches de 10 %, ou de 25 % (appelés dans ce cas « quartiles »). A noter que la médiane n’est rien d’autre que le quantile 50 % ; le quantile 0 % représente la prévision donnant le moins de précipitations et le quantile 100 % l’extrême opposé.
• A partir de tous ces éléments, il est possible de calculer des probabilités. A MétéoSuisse, nous utilisons généralement cet outil pour évaluer les probabilités de dépasser certains seuils, en particulier pour les avertissements.

Exemples concrets

Evidemment, dans la réalité, la distribution des précipitations n’est jamais symétrique. Pour la commune de Crissier et en situation orageuse de marais barométrique par exemple, la prévision des 51 membres s’apparenterait plutôt à une distribution telle que ci-dessous (la plupart des membres ne donne aucune précipitation, et quelques-uns en donnent beaucoup) :

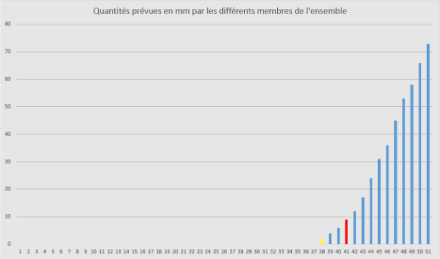
• Moyenne : 9 mm (en rouge)
• Écart-type : 19 mm
• Médiane (membre 26) : 0 mm
• Quantile 75 % : 3 mm (en jaune)

Dans une situation comme celle-ci, on voit tout de suite que la valeur moyenne de 9 mm n’est pas représentative, car la grande majorité des membres ne prévoient pas de précipitations (l’écart-type est d’ailleurs très important). On voit également que la médiane et la moyenne n’ont pas la même valeur, car la distribution n’est pas symétrique ; en l’occurrence, la médiane – valant 0 mm – donne une indication utile car elle est identique à la grande majorité des membres. La valeur de 3 mm pour le quantile 75 % indique que seuls 25 % des membres prévoient plus de 3 mm. On peut donc en conclure qu’il est fort probable que la commune de Crissier passe entre les gouttes, mais il n’est pas exclu non plus qu’un orage stationnaire déverse sur elle plus de 70 mm en très peu de temps.

A l’inverse, le passage d’un puissant front quasi-stationnaire pourrait faire l’objet d’une distribution telle que ci-dessous :

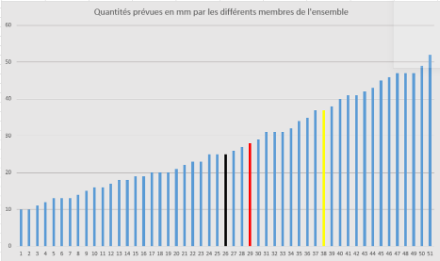
• Moyenne : 28 mm (représentée par le membre 29 en rouge)
• Écart-type : 12 mm
• Médiane : 25 mm (en noir)
• Quantile 75 % : 37 mm (en jaune)

Dans une situation comme celle-ci, la probabilité d’avoir des précipitations est très élevée, mais une incertitude assez grande est présente concernant les cumuls exacts, la différence entre les deux extrêmes étant de plus de 40 mm ; l’écart-type est d’ailleurs significatif avec 12 mm. La distribution est assez symétrique, moyenne et médiane étant très proches. En prévision, il serait assez logique dans un tel cas de tabler sur des valeurs comprises entre 20 et 30 mm.

L’expression des probabilités à MétéoSuisse

Voyons, à l’aide des différents termes statistiques mentionnés, quelle est la prévision du modèle COSMO-2E, dont l’ensemble compte 21 membres, pour les cumuls de pluie entre mardi 4 et mercredi 5 juillet à 18 UTC. Pour les prévisions de pluie, la moyenne n’est pas intéressante, car elle sera toujours non nulle dès que des précipitations seront présentes, ne serait-ce que dans un seul membre ; elle n’est dès lors pas utilisée. L’écart-type lui est en revanche significatif, car il nous donne une indication sur la fiabilité de la prévision.

Les membres de l’ensemble

Il s’agit de 21 prévisions différentes pour une même échéance et un même paramètre, à partir de conditions initiales légèrement modifiées :

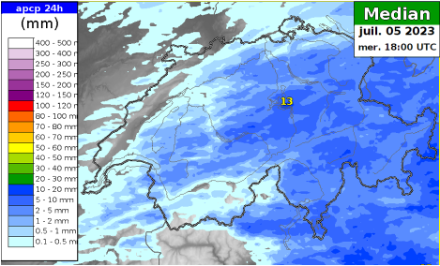
La médiane

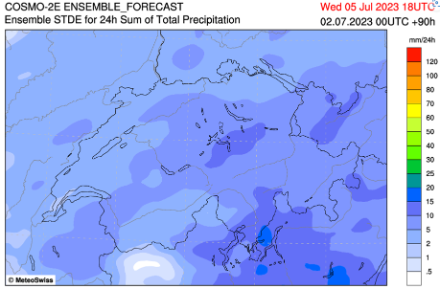
L'écart-type

Les quantiles

Les probabilités

Les probabilités pour un point donné

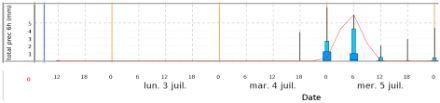
Pour un point donné (ici Aigle pour les ensembles du modèle COSMO-2), les probabilités se présentent comme ci-dessous. Les quantiles 0 et 100 % sont représentés par des barres verticales, les quantiles 90-75 % et 10-25 % par des rectangles bleus ciel étroits, le quantile 25-75 % par un rectangle bleu foncé large et la médiane par un trait noir horizontal. D’une manière générale, plus la « boîte » bleue est étendue, plus la dispersion est grande et la prévision est incertaine.

Conclusion

Si les membres de la prévision d’ensemble ont une grande cohérence météorologique car ils obéissent à un scénario précis, il n’en va pas de même pour les outils dérivés tels que médiane, quantiles, etc…. Par exemple, la carte du quantile 100 % des précipitations montre pour chaque pixel la valeur la plus élevée, indépendamment des scénarii météorologiques à l’origine de cette valeur. Ainsi, le scénario donnant le maximum de précipitation à Crissier n’est pas forcément le même que celui donnant le maximum à Zürich, et pourtant les deux figurent sur la même carte ; il en va de même pour la moyenne ou l’écart-type.

On le voit, les probabilités sont une approche incontournable des prévisions météorologiques modernes, mais elles donnent leur pleine mesure à condition d’être couplées à des approches plus classiques, à des notions climatologiques, à l’expérience humaine, à la connaissance du terrain ainsi qu’à celle des forces et faiblesses des différents modèles.

C’est là que le météorologue intervient désormais…